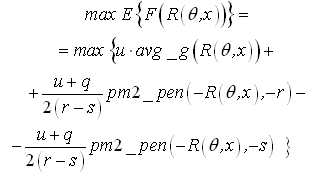Formal Problem Statement CS_Optimization_Utilities
Notations
I = number of instruments in portfolio; i = {1,…,I} index of instruments in portfolio;
J = number of scenarios; j = {1,…,J} index of scenarios;
![]() = portion of wealth invested in instrument i, i = {1,…,I};
= portion of wealth invested in instrument i, i = {1,…,I};
![]() = vector of decision variables;
= vector of decision variables;
![]() = lower bound on portion of wealth invested in instrument i, i = {1,…,I};
= lower bound on portion of wealth invested in instrument i, i = {1,…,I};
![]() = upper bound on wealth invested in instrument i, i = {1,…,I};
= upper bound on wealth invested in instrument i, i = {1,…,I};
![]() = price of instrument i at initial time 0;
= price of instrument i at initial time 0;
![]() = price-vector at initial time 0;
= price-vector at initial time 0;
![]() = price of instrument i for scenario j at time 1;
= price of instrument i for scenario j at time 1;
![]() = rate of return of instrument i for scenario j;
= rate of return of instrument i for scenario j;
![]() = return of instrument i for scenario j;
= return of instrument i for scenario j;
![]() = random value having J equally probable scenarios of rates of return,
= random value having J equally probable scenarios of rates of return, ![]() ;
;
![]() = random value having J equally probable scenarios of returns,
= random value having J equally probable scenarios of returns, ![]()
![]() = random vector of rates of return;
= random vector of rates of return;
![]() = random return vector;
= random return vector;
![]() = vector of rates of return for scenario j;
= vector of rates of return for scenario j;
![]() = return vector for scenario j;
= return vector for scenario j;
|
= rate of return of the portfolio for scenario j; |
|
= return of the portfolio for scenario j; |
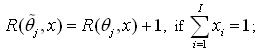
|
= Average Gain function; |
|
=Partial Moment Two Penalty |
function, where w is a threshold value;
|
= Exponential utility function, where a>0; |
|
= Logarithmic utility function; |
|
=Linear-Quadratic utility function, where |
F(R) = an appraisal (= monitoring) function, a linear-quadratic function modeling the decision maker attitude towards risk.
F(R) is defined as follows:
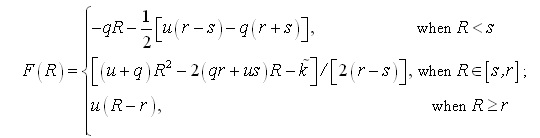
r = the hurdle rate;
s = the sub-hurdle rate, s < r;
u, q =constants, q < - u < 0;
![]()
The function F(R) can be represented as follows:
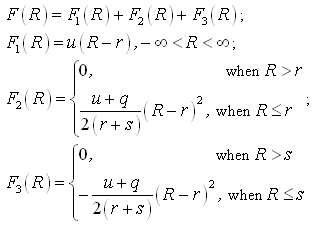
Optimization Problem 1
Maximizing Exponential Utility
|
(CS.1) |
subject to
budget constraint
|
(CS.2) |
bounds on positions
|
(CS.3) |
Optimization Problem 2
Maximizing Linear-Quadratic Utility
|
(CS.4) |
subject to
budget constraint
|
(CS.5) |
bounds on positions
|
(CS.6) |
Optimization Problem 3
Maximizing Logarithmic Utility
|
(CS.7) |
subject to
budget constraint
|
(CS.8) |
bounds on positions
|
(CS.9) |
Initial Data
Number of instruments in the portfolio, I = 12;
Number of scenarios, J = 199554;
Values of parameters:
q = -20;
u = 1;
r = 10;
s = 3.