Example of Optimization Problem
Contents
Recourse Function:
is the first stage decision vector;
is the vector of the second stage variables.
is the number of scenarios of the recourse function.
Scenario values for random parameters in the second stage:
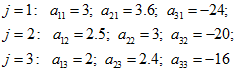
Value of Recourse function on scenario 
:
,
subject to
second stage constraints
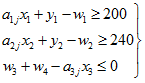
box constraints on the second stage decision variables
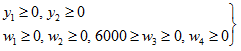
Two-stage stochastic programming optimization problem (with Recourse Function):
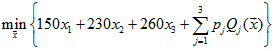
subject to
first stage constraint
constraints on the first stage decision variables
.
Problem Statement in Run-File Environment:
minimize
linear(matrix_x_obj)
avg(recourse(matrix_xfirst_1, matrix_subproblem_1,matrix_of_scenarios_1))
Constraint: <= 500
linear(matrix_budget)
Box: >= 0
Note. String “Box: >= 0” defines lower bounds only for the first stage variables. Bounds for the second stage variables are in matrix_subproblem_1.
Matrices with data:
matrix_x_obj:
x1 |
x2 |
x3 |
150 |
230 |
260 |
matrix_xfirst_1:
x1 |
x2 |
x3 |
0 |
0 |
0 |
Note. Gray color highlights the elements of the matrix which are not used for calculations.
matrix_subproblem_1:
x1 |
x2 |
x3 |
y1 |
y2 |
w1 |
w2 |
w3 |
w4 |
lower_bounds |
upper_bounds |
0 |
0 |
0 |
238 |
210 |
-170 |
-150 |
-36 |
-10 |
0 |
0 |
2.5 |
0 |
0 |
1 |
0 |
-1 |
0 |
0 |
0 |
200 |
1e+20 |
0 |
3 |
0 |
0 |
1 |
0 |
-1 |
0 |
0 |
240 |
1e+20 |
0 |
0 |
-20 |
0 |
0 |
0 |
0 |
1 |
1 |
-1e+20 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
1e+20 |
1e+20 |
1e+20 |
1e+20 |
6000 |
1e+20 |
0 |
0 |
Note. Gray color highlights the elements of matrix which are not used for calculations.
matrix_of_scenarios_1:
x1(2) |
x2(3) |
x3(4) |
scenario_probability |
3 |
3.6 |
-24 |
0.333333333333 |
2.5 |
3 |
-20 |
0.333333333333 |
2 |
2.4 |
-16 |
0.333333333333 |
matrix_budget:
x1 |
x2 |
x3 |
1 |
1 |
1 |
Solution report for described problem:
Problem: solution_status = optimal
Timing: Data_loading_time = 0.03, Preprocessing_time = 0.05, Solving_time = 0.00
Variables: optimal_point = point_problem_1
Objective: = -108390.000000000000
Constraint: = 5.000000000000e+002 [5.684341886081e-014]
Function: linear(matrix_x_obj) = 1.089000000000e+005
Function: avg(recourse(matrix_xfirst, matrix_subproblem,matrix_of_scenarios)) = -2.172900000000e+005
Function: linear(matrix_budget) = 5.000000000000e+002
Optimal point:
Component_name Value
x1 1.700000000000e+002
x2 8.000000000000e+001
x3 2.500000000000e+002