External m-functions for Function and Gradient
The definition and the use of External Functions (thereafter — functions) complies with the following rules:
| 1. | User can define his/her own functions and use them in an optimization problem. |
| 2. | The total number of function arguments should not exceed 16. |
| 3. | The total number of symbols in the function description should not exceed 128. |
| 4. | The function name must begin with the prefix fnext_. |
| 5. | The function definition can include only legal symbols (ref. to the definition of legal symbols in the PSG Help). |
| 6. | Functions must return a scalar value. |
| 7. | User should define for each function the corresponding gradient function, with the same name and arguments set. |
| 8. | The gradient function name must begin with the prefix grext_. For example, the fnext_myfunction(arg1, arg2, arg3) function must have the corresponding grext_myfunction(arg1, arg2, arg3) function for gradient calculation. |
| 9. | The gradient function must return a vector value, with dimension equals to the number of variables (not arguments) on which the function is defined. |
| 10. | External Function and its gradient must be implemented in different m-files that have the name (after an appropriate prefix) coinciding with the name of the function and its gradient. |
| 11. | The function and its gradient must have the same list of arguments. |
| 12. | The arguments types are legal MATLAB data types. |
| 13. | Only variables of the problem can be used as arguments of the functions (numerical values are not allowed) |
| 14. | All function arguments must be defined before calling the optimization procedure. |
| 15. | Argument names are case sensitive. |
| 16. | The first function argument must be a string with the tab separated list of variables names, on which the function is defined. |
| 17. | The second function argument must be a real vector (row vector or column vector) of components ordered as the sequence of the variables passed as the first argument. The second argument is a variable point at which the value of the function is calculated during the optimization. The actual value of this point must correspond to the function and its gradient definition domain. |
| 18. | The problem statement (see Problem Statement Description in MATLAB) must include the complete function definition (with its three arguments). |
| 19. | External functions (and their linear combinations) can be specified in the objective and constraints. |
| 20. | External functions can be used by the PSG functions tbpsg_run, riskprog and riskconstrprog for solving the optimization problems. |
Example. Formal Problem Statement
Minimizing
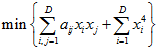
subject to
![]()
box constraints
![]()
To solve the problem we created files fnext_polynom_m.m and grext_polynom_m.m (in the folder .\Aorda\PSG\MATLAB\Examples\Problems\) containing function code:
function [value] = fnext_polynom_m(headerpoint, valuespoint, matrix_A)
D = length(valuespoint);
if (size(matrix_A, 1) ~= D) || (size(matrix_A, 2) ~= D)
error('Wrong sizes of matrix_A');
end
value = 0.0;
for i = 1:D
for j = 1:D
value = value + matrix_A(i, j)*valuespoint(i)*valuespoint(j);
end
value = value + valuespoint(i)^4;
end
end
and gradient code:
function [grvalue] = grext_polynom_m(headerpoint, valuespoint, matrix_A)
D = length(valuespoint);
if (size(matrix_A, 1) ~= D) || (size(matrix_A, 2) ~= D)
error('Wrong sizes of matrix_A');
end
grvalue = zeros(1, D);
for i = 1:D
for j = 1:D
grvalue(i) = grvalue(i) + matrix_A(i, j)*valuespoint(j);
end
grvalue(i) = grvalue(i) + 4*valuespoint(i)^3;
end
end
Solving the problem using mpsg_solver function
Run the following example from the folder ./Aorda/PSG/MATLAB/Examples/Problems/External_Function_test.m or type the next code in MATLAB:
Define problem dimension:
D = 5;
Create the tab separated list of variables names (x1..xD):
headerpoint = ['x1' sprintf('\tx%d', 2:D)];
Create row vector for verifying calculation of the function and the gradient:
thispoint = ones(1, D);
Define the matrix on which the function and the gradient are calculated:
A = eye(D);
for i=1:D-1
A(i, i+1) = 1.0/(10.0+D);
A(i+1, i) = A(i, i+1);
end
Define the matrix on which the constraint is defined:
headermatrix = ['id' sprintf('\t%s', headerpoint)];
matrix_linear = ones(1, D+1);
Specify the problem description:
problem_statement = sprintf('%s\n',...
'Problem: problem_test, type = minimize',...
'Objective: objective_external_function',...
'fnext_polynom_m(headerpoint, thispoint, A)',...
'Constraint: constraint_linear, lower_bound = 0, upper_bound = 0',...
'linear_balance(matrix_linear)',...
'Box_of_Variables: lowerbounds = -1, upperbounds = 1',...
'Solver: TANK, precision = 9');
Pack the matrix_linear matrix into the structure array defining the initial data using tbpsg_matrix_pack:
count = 1;
toolboxstruc_arr(count) = tbpsg_matrix_pack('matrix_linear', matrix_linear, headermatrix);
Solve the problem using tbpsg_run:
[solution_str, outargstruc_arr] = tbpsg_run(problem_statement, toolboxstruc_arr);
Output:
fprintf('Solution status: %s\n%s\nOptimal point:\n', get_solution(solution_str, outargstruc_arr, 'solution_status'), ...
get_solution(solution_str, outargstruc_arr, 'objective'));
optimal_point = get_optimalpoint(solution_str, iargstruc_arr, outargstruc_arr);
for i=1:D
fprintf('%s\t=\t%f\n', optimal_point{i, 1}, optimal_point{i, 2});
end
After running the function the following messages are displayed:
mpsg_solver function using:
Reading problem formulation
Reading fnext_polynom_m(headerpoint, thispoint, a)
Reading matrix_linear
16.7% of scenarios is processed
Start optimization
Ext.iteration=7 Objective=0.000000000000E+00 Residual=0.000000000000E+00
Optimization was stopped
Solution is optimal
Calculating resulting outputs. Writing solution.
Solver has normally finished. Solution was saved.
Solution status: optimal
objective_external_function = 0
Optimal point:
x1 = 0.000000
x2 = 0.000000
x3 = 0.000000
x4 = 0.000000
x5 = 0.000000
Solving the problem using riskprog function
We can solve the same problem using riskprog function (see riskprog).
[xout, fval, status] = riskprog('fnext_polynom_m(headerpoint, thispoint, A)', ...
[], [], [], [], [], [], [], matrix_linear(1, 2:end), 0, -1, 1);
The first argument of the riskprog function is the complete function description defining the objective function (the string 'fnext_polynom_m(headerpoint, thispoint, A)').
Since the risk function is an External Function, parameters w, H, c, p, d are not defined and should be omitted (defined as []).
The problem does not have equality constraints, thus parameters A and b are omitted.
As Aeq we substitute the matrix_linear matrix defined before (without the first column where id is defined). The matrix_linear defined above is the matrix of coefficients for the inequality constraints. The first column of this matrix, which represents the 'id" column, is not needed in the riskprog function.
The right-hand side of the inequality constraints is defined as 'null' vector.
Box constraints are specified as -1 and 1 for all the components of the solution vector.
After running the function the following messages are displayed:
riskprog function using:
Solution status: optimal
Objective = 0.000000
Optimal point:
x1 = 0.000000
x2 = 0.000000
x3 = 0.000000
x4 = 0.000000
x5 = 0.000000
In a similar way, External Functions can be used in the riskconstrprog function (see riskconstrprog).
