Mean Absolute Risk for Gain Normal Dependent (meanabs_risk_nd_g)
Contents
Mean Absolute Risk for Gain Normal Dependent. Mean Absolute for Gain when all coefficients in Linear Loss function are mutually dependent normally distributed random values. (Mean Absolute for Gain Normal Dependent) = - Average Loss + Mean Absolute Deviation.
Syntax
meanabs_risk_nd_g(matrix_mn,matrix_cov) |
short call |
meanabs_risk_nd_g_name(matrix_mn,matrix_cov) |
call with optional name |
Parameters
matrix_mn is a PSG matrix of mean values:
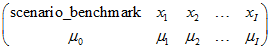
where the header row contains names of variables. The second row contains numerical data.
matrix_cov is a PSG matrix of covariance values:
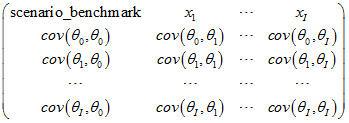
where the header row contains names of variables. Other rows contain numerical data.
Mathematical Definition
Mean Absolute Risk for Gain Normal Dependent function is calculated as follows:
,
where
is Mean Absolute Deviation Normal Dependent function,
,
,
is probability density function of the standard normal distribution.
is an argument of Mean Absolute Risk for Gain Normal Dependent function.
Example
See also
Mean Absolute Error, Mean Absolute Error Normal Independent, Mean Absolute Error Normal Dependent, Mean Absolute Risk, Mean Absolute Risk for Gain, Mean Absolute Risk Normal Independent, Mean Absolute Risk for Gain Normal Independent, Mean Absolute Risk Normal Dependent, Mean Absolute Deviation, Mean Absolute Deviation Normal Independent, Mean Absolute Deviation Normal Dependent