Mean Square Error Normal Independent (meansquare_ni)
Contents
Mean Square Error Normal Independent. Mean Square error of Linear Loss with independent normally distributed random coefficients. It is calculated with Matrix of Means (one row matrix) and Matrix of Variances (one row matrix).
Syntax
meansquare_ni(matrix_mn,matrix_vr) |
short call; |
meansquare_ni_name(matrix_mn,matrix_vr) |
call with optional name. |
Parameters
matrix_mn is a PSG matrix of mean values:
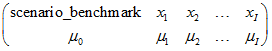
where the header row contains names of variables. The second row contains numerical data.
matrix_vr is a PSG matrix of variance values:
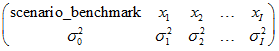
where the header row contains names of variables. The second row contains numerical data.
Mathematical Definition
Mean Square Error Normal Independent function is calculated as follows:
,
where
is a mean of the loss function;
is a variance of the loss function.
is Loss Function (See section Loss and Gain Functions);
is an argument of function.
Example
See also
Root Mean Squared Error, Root Mean Squared Error Normal Independent, Root Mean Squared Error Normal Dependent, Standard Risk, Standard Gain, Standard Risk Normal Independent, Standard Gain Normal Independent, Standard Risk Normal Dependent, Standard Gain Normal Dependent, Standard Deviation, Mean Square Error, Mean Square Error Normal Dependent, Variance