Partial Moment Two Max Deviation for Gain (pm2_max_dev_g)
Contents
Partial Moment Two Max Deviation for Gain. There are M Linear Loss scenario functions (every Linear Loss scenario function is defined by a Matrix of Scenarios). A new Maximum Deviation for Gain scenarios function is calculated by maximizing losses over -(Linear Loss)+(Expected Linear Loss) functions (over M functions for every scenario). Partial Moment Two Max Deviation for Gain is calculated by taking Partial Moment Two of the Maximum Deviation for Gain scenarios.
Syntax
pm2_max_dev_g(w,matrix_1,matrix_2,...,matrix_M) |
short call |
pm2_max_dev_g_name(w,matrix_1,matrix_2,...,matrix_M) |
call with optional name |
Parameters
matrix_m is a Matrix of Scenarios:
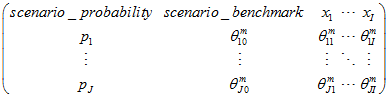
where the header row contains names of variables (except scenario_probability, and scenario_benchmark). Other rows contain numerical data. The scenario_probability, and scenario_benchmark columns are optional. 
.
 | is a threshold value. |
Mathematical Definition
Partial Moment Two Max Deviation for Gain function is calculated as follows:
,
where:
is Partial Moment Two Deviation for Loss function,
M = number of random Loss Functions 
,
= vector of random coefficients for m-th Loss Function;
= j-th scenario of the random vector 
,
is a random function with scenarios 
,
is an argument of function.
Every Loss Function is defined by a separate matrix of scenarios and has an equal number of scenarios J.
Probability 
of scenario 
is defined by the first matrix.
Example
See also