Partial Moment Two Max (pm2_max_pen)
Contents
Partial Moment Two Max. There are M Linear Loss scenario functions (every Linear Loss scenario function is defined by a Matrix of Scenarios). A new Maximum Loss scenarios function is calculated by maximizing losses over Linear Loss functions (over M functions for every scenario). Partial Moment Two Max is calculated by taking Partial Moment Two of the Maximum Loss scenarios.
Syntax
pm2_max_pen(w,matrix_1,matrix_2,...,matrix_M) |
short call |
pm2_max_pen_name(w,matrix_1,matrix_2,...,matrix_M) |
call with optional name |
Parameters
matrix_m is a Matrix of Scenarios:
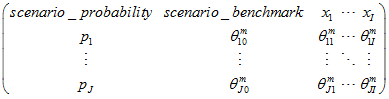
where
,
where the header row contains names of variables (except scenario_probability, and scenario_benchmark). Other rows contain numerical data. The scenario_probability, and scenario_benchmark columns are optional.
 | is a threshold value. |
Mathematical Definition
Partial Moment Two Max function is calculated as follows
,
where:
is Partial Moment Two Penalty for Loss function,
M = number of random Loss Functions (See section Loss and Gain Functions):
,
= vector of random coefficients for m-th Loss Function;,
= j-th scenario of the random vector 
,
is a random function with scenarios:
,
is an argument of function.
Every Loss Function is defined by a separate matrix of scenarios and has an equal number of scenarios J.
Probability 
of scenario 
is defined by the first matrix.
Example
See also
Partial Moment Group, Partial Moment Two Max for Gain.