Probability of Exceedance Multiple Normal Dependent (prmulti_pen_nd)
Contents
Probability of Exceedance Multiple Normal Dependent. There are M Linear Loss functions with mutually dependent normally distributed random coefficients. Probability of Exceedance Multiple Normal Dependent = 1-(Probability that all M Linear Loss functions are below the threshold).
Syntax
prmulti_pen_nd(w,matrix_mn,matrix_cov_1,...,matrix_cov_M) |
short call; |
prmulti_pen_nd_name(w,matrix_mn,,matrix_cov_1,...,matrix_cov_M) |
call with optional name. |
Parameters
is a threshold value.
matrix_mn is a PSG matrix of mean values of coefficients of Loss functions:
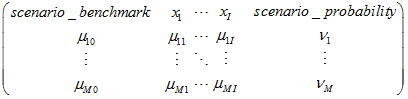
where the header row contains names of variables. Other rows contain numerical data.
matrix_cov_m is a PSG matrix of covariance values of coefficients of m-Loss function:
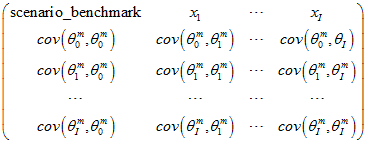
where the header row contains names of variables. Other rows contain numerical data.
,
Mathematical Definition
The Probability of Exceedance Multiple Normal Dependent is calculated as follows:
.
where
;
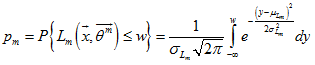is average of Loss Functions;
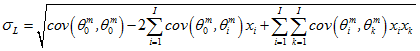is standard Deviation of Loss Functions;
is 
-th Loss Function (See section Loss and Gain Functions);
is an argument of function.
Example
See also
Probability Group, Probability of Exceedance for Gain Multiple Normal Dependent.