Solution in MATLAB Environment
Table 1. Solution report for Problem 1
Figure 1. Cube spline with 5 pieces
Table 2. Solution report for Problem 2
Table 3. Values of logexp_sum for sum of splines
Case study Binary Classification with Splines (see Formal Problem Statement) in MATLAB Environment is solved with tbpsg_run PSG function.
Three problems are included:
| • | Problem 1 (CS.1): one factor approximation with spline. |
| • | Problem 2 (CS.2): estimation sum of splines for a set of factors. |
| • | Problem 3 (CS.3): estimation sum of splines with cross validation technique. |
tbpsg_run PSG function is used.
MATLAB code for Binary Classification with Splines is in file CS_Binary_Classification_with_Splines_Toolbox.m.
Data are saved in files CS_Binary_Classification_with_Splines_data_Toolbox.mat.
Let us describe the main operations. To run case study you need to do the following main steps:
In file CS_Binary_Classification_with_Splines_Toolbox.m:
%Load data saved in PSG Toolbox format in structure:
load 'CS_Binary_Classification_with_Splines_data_Toolbox.mat' 'toolboxstruc_arr'
%Save variables from structure toolboxstruc_arr to Workspace:
psg_export_to_workspace(toolboxstruc_arr);
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
% Problem 1: one spline
% Choose one factor for construction of one spline
toolboxstruc_arr_f1(1)=tbpsg_matrix_pack('matrix_vars_f1', toolboxstruc_arr(1).data.data(:,1), 'f1');
toolboxstruc_arr_f1(2)=tbpsg_matrix_pack('matrix_data_f1', [toolboxstruc_arr(2).data.data(:,1),toolboxstruc_arr(2).data.bench], {'f1','scenario_benchmark'});
% Problem statement for estimation of one spline
problem_statement = sprintf('%s\n',...
'Problem: problem_logexp_of_spline, type = maximize',...
'logexp_sum(spline_sum(matrix_vars_f1, matrix_data_f1))',...
'Problem: problem_calculate, type = calculate',...
'Point: point_problem_logexp_of_spline',...
'spline_sum(matrix_vars_f1, matrix_data_f1, matrix_data_f1_knots)',...
'logexp_sum(spline_sum(matrix_vars_f1, matrix_data_f1, matrix_data_f1_knots))');
% Uncomment the following line to open the problem in Toolbox Window
%tbpsg_toolbox(problem_statement,toolboxstruc_arr_f1);
%Optimize problem:
[solution_str, outargstruc_arr] = tbpsg_run(problem_statement, toolboxstruc_arr_f1);
%Display solution
disp(' ')
disp('Solution report for Problem 1')
disp(solution_str(1).solution)
disp(' ')
loss_data = tbpsg_vector_data(solution_str, outargstruc_arr);
dependent_data=toolboxstruc_arr(2).data.bench;
independent_data=toolboxstruc_arr(2).data.data(:,1);
loc=sortrows([independent_data,loss_data-dependent_data],1);
% Find knots
quants=outargstruc_arr{2}(4).values(1:end-1);
nodesvalue_x=[];nodesvalue_y=[];pos=0;
for i=1:size(quants,1)
pos=pos+quants(i);
nodesvalue_y=[nodesvalue_y,loc(pos,2)];%loss_data(pos)-dependent_data(pos)
nodesvalue_x=[nodesvalue_x,loc(pos,1)];%independent_data(pos)
end
% Plot estimated spline
h1 = figure;
plot(loc(:,1),loc(:,2));
hold on
plot(nodesvalue_x,nodesvalue_y,'*','MarkerSize',10,'Color',[1 0 0]);
title('Cube spline with 5 pieces')
xlabel('Independent Factor')
ylabel('Spline')
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
% Problem 2: classificator on the basis of sum of splines
%Generate problem statement:
clear problem_statement;
problem_statement = sprintf('%s\n',...
'Problem: problem_logexp_sum_of_splines, type = maximize',...
'logexp_sum(spline_sum(matrix_parameters_vars, matrix_data))',...
'Problem: problem_calculate, type = calculate',...
'Point: point_problem_logexp_sum_of_splines',...
'logexp_sum(spline_sum(matrix_parameters_vars, matrix_data, matrix_data_knots))',...
'logistic(spline_sum(matrix_parameters_vars, matrix_data, matrix_data_knots))',...
'spline_sum(matrix_parameters_vars, matrix_data, matrix_data_knots)');
%Optimize problem:
[solution_str, outargstruc_arr] = tbpsg_run(problem_statement, toolboxstruc_arr);
%Display solution
disp(' ')
disp('Solution report for Problem 2')
disp(solution_str(1).solution)
disp(' ')
%Plot probabilities of classification
sum_splines = tbpsg_vector_data(solution_str, outargstruc_arr);
h2 = figure;
plot(sum_splines.logistic)
title('Probabilities obtained by spline classification')
xlabel('n')
ylabel('Probability')
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
% Problem 3: Cross Validation for sum of splines
clear problem_statement;
problem_statement = sprintf('%s\n',...
'for {matrix_fact_in; matrix_fact_out; #n}=crossvalidation(4, matrix_data) ',...
'Problem: problem_logexp_sum_of_splines_#n, type = maximize',...
'logexp_sum(spline_sum(matrix_parameters_vars, matrix_fact_in))',...
'Problem: problem_calculate_cv_#n, type = calculate',...
'Point: point_problem_logexp_sum_of_splines_#n',...
'logistic_1_#n(spline_sum(matrix_parameters_vars, matrix_fact_in, matrix_data_knots_in))',...
'logistic_2_#n(spline_sum(matrix_parameters_vars, matrix_fact_out, matrix_data_knots_in))',...
'logexp_sum_in_#n(spline_sum(matrix_parameters_vars, matrix_fact_in, matrix_data_knots_in))',...
'logexp_sum_out_#n(spline_sum(matrix_parameters_vars, matrix_fact_out, matrix_data_knots_in))',...
'end for');
%Optimize problem:
[solution_str, outargstruc_arr] = tbpsg_run(problem_statement, toolboxstruc_arr);
%Display solution
[output_structure] = tbpsg_solution_struct(solution_str, outargstruc_arr);
in_sample_obj=[];out_of_sample_obj=[];
for i=1:size(output_structure.function_name,1)/3
in_sample_obj=[in_sample_obj,output_structure.function_value(i*3-1)];
out_of_sample_obj=[out_of_sample_obj,output_structure.function_value(i*3)];
end
disp(' ')
line0='Values of logexp_sum for sum of splines';
line1='Data ';line2='In-Sample ';line3='Out-of-Sample';
for j=1:size(output_structure.function_name,1)/3
line1=sprintf('%s\t part %g ',line1,j);
line2=sprintf('%s\t%f',line2,in_sample_obj(j));
line3=sprintf('%s\t%f',line3,out_of_sample_obj(j));
end
sprintf('%s\n%s\n%s\n%s\n',line0,line1,line2,line3)
Table 1. Solution report for Problem 1
Problem: solution_status = optimal
Timing: Data_loading_time = 0.01, Preprocessing_time = 0.01, Solving_time = 0.12
Variables: optimal_point = point_problem_logexp_of_spline
Objective: = -0.688993804187
Constraint: constraint_for_smoothing_spline = -1.421085471520e-014, [1.421085471520e-014]
Function: logexp_sum(spline_sum(matrix_vars_f1, matrix_data_f1)) = -6.889938041872e-001
Figure 1. Cube spline with 5 pieces
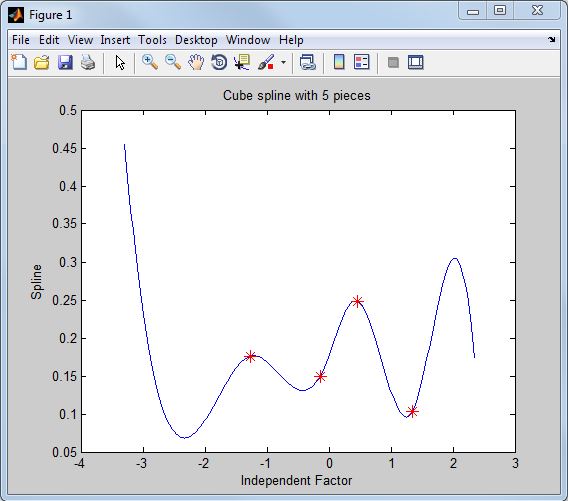
Table 2. Solution report for Problem 2
Problem: solution_status = optimal
Timing: Data_loading_time = 0.00, Preprocessing_time = 0.06, Solving_time = 18.01
Variables: optimal_point = point_problem_logexp_sum_of_splines
Objective: = -0.678139775164
Constraint: constraint_for_smoothing_spline = -1.062261389961e-012, [1.062261389961e-012]
Function: logexp_sum(spline_sum(matrix_parameters_vars, matrix_data)) = -6.781397751637e-001
Table 3. Values of logexp_sum for sum of splines
Data part 1 part 2 part 3 part 4
In-Sample -0.677323 -0.675272 -0.675020 -0.676921
Out-of-Sample -0.702592 -0.701651 -0.703571 -0.699656
