Description

MATLAB code

Results

Table 1. Summary table of performance of portfolios

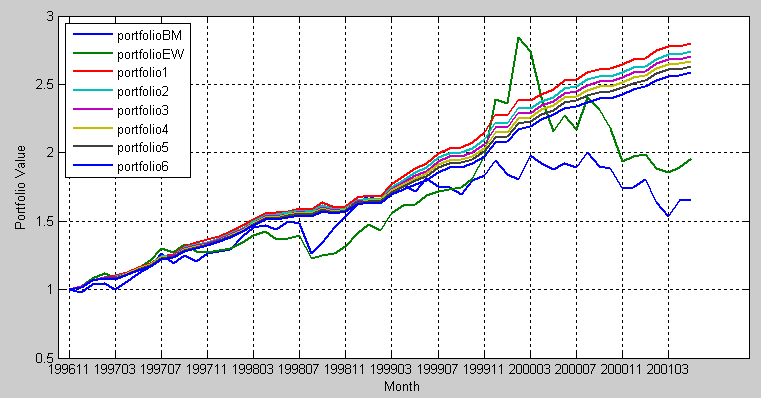
Figure 1. Graph comparing performance of portfolios

 

Description

Case study Investment Strategies for Portfolio of Hedge Funds (see (CS.5) - (CS.8) Formal Problem Statement) in MATLAB Environment is solved with riskrprog PSG subroutine.

 

MATLAB code

Let us describe the main operations. To run case study you need to do the following main steps in file CS_HedgeFunds_RiskInObjective_riskprog_variance.m.

 

Set TYPE parameter:

 

% TYPE='RISK' to optimize portfolio with risk in objective

% TYPE='VARIANCE' to optimize portfolio with variance in objective

TYPE = 'VARIANCE';

 

Initial settings:

 

InitialPortfolioValue = 10000.0; % initial value of portfolio

BudgetBound = 1.0; % budget bound

K = 0.000001; % K value in risk neutrality constraint

FirstInsampleIndex = 1;

InsampleSize = 12; % in sample set

DefaultLambda = 1.0; % default lambda value

VariablesLowerBound = 0.0; % lower box bounds

VariablesUpperBound = 0.1; % upper box bounds

Precision = 4; % default precision

Stages = 30;

BestFundsNumber = 20; % the number of the best returns funds in portfolioEW

SaveSolutionFile = 1; % set this key to write solving statistics to file solution_HedgeFunds.txt

 

Read funds and benchmark matrices:

 

clear header_main; clear date_vec; clear fundsdata_arr; clear variables_arr;

[header_main, date_vec, fundsdata_arr] = read_mainmatrix('matrix_fundreturns.txt');

clear header_bench; clear datebench_vec; clear benchdata_arr;

NumFunds = length(fundsdata_arr);

[header_bench, datebench_vec, benchdata_arr] = read_mainmatrix('matrix_benchmarkreturns.txt');

if (length(benchdata_arr) ~= length(date_vec))

   Error('Benchmark set is wrong');

end

 

fundsdata_arr = fundsdata_arr(:, 2:end);

benchdata_arr = benchdata_arr(:, 2:end);

 

Specify the structure and parameters for equally weighted and benchmark portfolios:

 

clear portfolio;

portf_count = 1;

portfolio(portf_count).name = 'portfolioBM'; % benchmark portfolio

portfolio(portf_count).type = 'benchmark';

portfolio(portf_count).lambda = 0; % no risk constraint

portfolio(portf_count).riskfunction = ''; % no risk constraint

portfolio(portf_count).riskfunction_parameter = []; % no risk constraint

portfolio(portf_count).modification = @(x) x; % no risk constraint

portf_count = portf_count+1;

portfolio(portf_count).name = 'portfolioEW'; % predefined equal weighted portfolio

portfolio(portf_count).type = 'ew';

portfolio(portf_count).lambda = 0; % not risk constrained

portfolio(portf_count).riskfunction = ''; % not risk constrained

portfolio(portf_count).riskfunction_parameter = []; % not risk constrained

portfolio(portf_count).modification = @(x) x; % not risk constrained

portf_count = portf_count+1;

 

Specify the structure and parameters for portfolios with risk measures:

 

if strcmp(TYPE, 'RISK')

 

Specify parameters for portfolios with some risk measures (which is NOT vriance). You should specify several values of the penalty coefficient in the lambda_list to have several trajectories with these coefficients. Currently only three values of the penalty coefficient are specified. According to these values, three optimal portfolios are generated with names "portfolio1", "portfolio2", and "portfolio3".

 

   lambda_list = [DefaultLambda 10*DefaultLambda 100*DefaultLambda]; % risk penalty coefficients

  for iportf=1:length(lambda_list)

       portfolio(portf_count).name = ['portfolio' num2str(iportf)]; % portfolio name like portfolio1, portfolio2, ...

       portfolio(portf_count).type = 'risk';

       portfolio(portf_count).lambda = lambda_list(iportf); % set your value of risk bound

       portfolio(portf_count).riskfunction = 'cvar_risk'; % set your risk measure

       portfolio(portf_count).riskfunction_parameter = 0.9; % set parameter of your risk measure

       portfolio(portf_count).modification = @(x) x; %

       portf_count = portf_count+1;

  end

else

 

Specify parameters for portfolios with Variance measure. You should specify several values of the penalty coefficient in the lambda_list to have several trajectories with these coefficients. Currently only three values of the penalty coefficient are specified. According to these values, three optimal portfolios are generated with names "portfolio1", "portfolio2", and "portfolio3".

 

   lambda_list = [0.1*DefaultLambda 0.125*DefaultLambda 0.2*DefaultLambda  0.25*DefaultLambda  0.4*DefaultLambda 0.7*DefaultLambda ]; % % variance penalty coefficients

  for iportf=1:length(lambda_list)

       portfolio(portf_count).name = ['portfolio' num2str(iportf)]; % portfolio names like portfolio1, portfolio2, ...

       portfolio(portf_count).type = 'risk';

       portfolio(portf_count).lambda = NumFunds*lambda_list(iportf); % set your value of risk bound

       portfolio(portf_count).riskfunction = 'variance'; % set your risk measure

       portfolio(portf_count).riskfunction_parameter = []; % there is no parameter in variance

       portfolio(portf_count).modification = @(x) sqrt(x); %

       portf_count = portf_count+1;

  end  

end

 

Specify settings for the first pass:

 

pass_count = 1;

outofsampleindex = FirstInsampleIndex+InsampleSize-1;

for iportf=1:length(portfolio)

   portfolio(iportf).returnportfolio(pass_count) = 0.0;

   portfolio(iportf).portfoliovalue(pass_count) = InitialPortfolioValue;

   portfolio(iportf).date(pass_count) = int32(str2num(cell2mat(date_vec{outofsampleindex})));

end

if SaveSolutionFile

   outfilename = 'solution_HedgeFunds_riskprog.txt';

   fsolid = fopen(outfilename, 'w');  

end

 

pass_count = pass_count+1;

outofsampleindex = outofsampleindex+1;

 

mpsg_suppress_message('On'); % PSG messages are swithced off

 

Begin generating several passes:

 

while outofsampleindex <= length(date_vec) % start main in sample - out of sample cycle

   fprintf('\nPass N%8d\n', pass_count);

 

During each pass the program specifies initial month of the in-sample period, FirstInsampleIndex, and its final month, outofsampleindex-1. The outofsample index specifies the out of sample month used for testing of the performance of the rebalanced portfolio. For in-sample period the program generates the following  data required for solving the optimization problem:    

"matrix_fundsreturns" containing scenarios of hedge funds returns needed for calculating Risk function included in the objective with the penalty coefficient.

 

   clear matrix_fundsreturns;

   matrix_fundsreturns = fundsdata_arr(FirstInsampleIndex:outofsampleindex-1, : );

 

"matrix_expectedreturns" needed for calculating expected return of portfolio included in the objective

 

   clear matrix_expectedreturns;

   matrix_expectedreturns = sum(matrix_fundsreturns)/size(matrix_fundsreturns, 1);

 

"matrix_budget" containing unit coefficients for budget constraint.

 

   clear matrix_budget;

   matrix_budget = ones(1, size(matrix_fundsreturns, 2));

 

Calculate "matrix_beta" containing coefficients for market-neutrality constraint:

 

   clear matrix_beta;

   matrix_funds = fundsdata_arr(FirstInsampleIndex:outofsampleindex-1,:);

   middle_funds = sum(matrix_funds)/size(matrix_funds, 1);

  for i=1:size(matrix_funds, 1)

       matrix_funds(i,:)=matrix_funds(i,:)-middle_funds;

  end

   vector_bench = benchdata_arr(FirstInsampleIndex:outofsampleindex-1);

   vector_bench = vector_bench - sum(vector_bench)/size(vector_bench, 1);

   bench_norm = vector_bench'*vector_bench;

   vector_bench = vector_bench/bench_norm;

   matrix_beta = (matrix_funds'*vector_bench)';

   portf_count = 1;

 

Start portfolio cycle:

 

  while portf_count <= length(portfolio)

       current_portfoliovalue = portfolio(portf_count).portfoliovalue(pass_count-1);

     

Generate problem statement for portfolio with risk measure:

 

      if (strcmp(portfolio(portf_count).type ,'risk'))

           risk = portfolio(portf_count).riskfunction;

           w = portfolio(portf_count).riskfunction_parameter;

           H = portfolio(portf_count).modification(portfolio(portf_count).lambda)/current_portfoliovalue*matrix_fundsreturns;

           c = []; p = [];

           d = -1.0/current_portfoliovalue*matrix_expectedreturns';

           A = [matrix_beta; -matrix_beta];

           b = [K*current_portfoliovalue; K*current_portfoliovalue];

           Aeq = matrix_budget;

           beq = BudgetBound*current_portfoliovalue;

           lb = current_portfoliovalue*VariablesLowerBound;

           ub = current_portfoliovalue*VariablesUpperBound;

           x0 = [];

          if strcmp(TYPE, 'RISK')

               options.Linearization = 'On';

               options.Solver = 'TANK';

          else

               options.Linearization = 'Off';

               options.Solver = 'VAN';

          end

           options.Precision = Precision; options.Stages = Stages;

Optimize problem  for portfolio with risk measure:

 

          [optimal_point, fval, solutionstatus, output] = riskprog (risk, w, H, c, p, d, A, b, Aeq, beq, lb, ub, x0, options);

         

For portfolio with risk measure, determine portfolio return and value corresponding to out of sample month:

 

           portfolio_return = fundsdata_arr(outofsampleindex, :)*optimal_point;

           portfolio(portf_count).portfoliovalue(pass_count) = current_portfoliovalue+portfolio_return;

           portfolio(portf_count).returnportfolio(pass_count) = portfolio_return;

           portfolio(portf_count).date(pass_count) = int32(str2num(cell2mat(date_vec{outofsampleindex})));

         

Save results for portfolio with risk measure in external file:

 

          if SaveSolutionFile

               fprintf(fsolid, 'Portfolio: %s, end date: %s, status: %s\n', portfolio(portf_count).name, ...

                   cell2mat(date_vec{outofsampleindex-1}), solutionstatus);

               fprintf(fsolid, 'Objective: %.6f\n', fval);

               fprintf(fsolid, 'Budjet Constraint: %.6f\nBetaneutrality Constraint: %.6f\n', output.fAeqval, output.fAval(1));

               fprintf(fsolid, '****************************************\n\n');

          end

      else

         

Determine benchmark portfolio return and value corresponding to out of sample month:

 

          if strcmp(portfolio(portf_count).type, 'benchmark')

               portfolio_return = benchdata_arr(outofsampleindex)*current_portfoliovalue;

               portfolio(portf_count).returnportfolio(pass_count) = portfolio_return;

               portfolio(portf_count).portfoliovalue(pass_count) = current_portfoliovalue+portfolio_return;

               portfolio(portf_count).date(pass_count) = int32(str2num(cell2mat(date_vec{outofsampleindex})));

          else

             

              if strcmp(portfolio(portf_count).type, 'ew')

 

Create equally weighted portfolio by including the best portfolio funds having maximum returns for in sample period. The number of the best funds in the portfolio is BestFundsNumber.

 

                   infundreturns = sum(matrix_fundsreturns);

                   outfundreturns = fundsdata_arr(outofsampleindex, :);

 

Determine equally weighted portfolio return and value corresponding to out of sample month:

 

                   [locarr, indexarr] = sort(infundreturns, 'descend');

                   portfolio_return = sum(outfundreturns(indexarr(1:BestFundsNumber)))*current_portfoliovalue/BestFundsNumber;

                   portfolio(portf_count).returnportfolio(pass_count) = portfolio_return;

                   portfolio(portf_count).portfoliovalue(pass_count) = current_portfoliovalue+portfolio_return;

                   portfolio(portf_count).date(pass_count) = int32(str2num(cell2mat(date_vec{outofsampleindex})));

              end

          end

      end

       portf_count = portf_count+1;

  end % end portfolio cycle

 

Specify settings for the next pass:

 

   outofsampleindex = outofsampleindex+1;

   pass_count = pass_count+1;

end % end main in sample - out of sample cycle

 

Results

Table 1. Summary table of performance of portfolios

 

 

Figure 1. Graph comparing performance of portfolios