subroutine
Table 1. Solution of Problem 1
Table 2. Solution of Problem 2
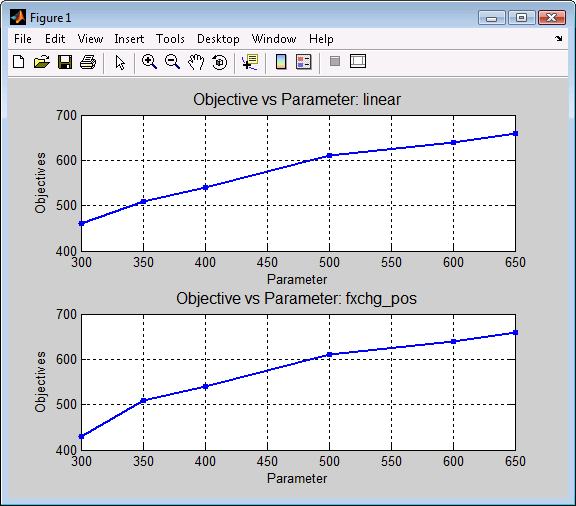
Figure 1. Objective vs Parameter for Problem 1 and Problem 2
Problem of optimization setup for a project selection problem in MATLAB Environment. Two optimization problems (see Formal Problem Statement) Problem 1 (CS.1) - (CS.3) and Problem 2 (CS.4) - (CS.6) are solved by PSG subroutine riskconstrparam.
Main MATLAB code is in file CS_Project_Selection_FXCHG_psg_riskconstrparam.m.
Data are saved in file CS_Project_Selection_FXCHG_riskconstrprog_data.mat.
Let us describe the main operations. To run case study you need to do the following main steps:
In file CS_Project_Selection_FXCHG_psg_riskconstrparam.m.
Load data from mat file:
load('CS_Project_Selection_FXCHG_riskconstrprog_data.mat');
Specifies a set of values of parameter (upper bound on init capital) for which runs should be conducted:
UB_Init_Capital = [300 350 400 500 600 650];
Set solver options:
options.Linearization = 'On';
options.Solver = 'CAR';
options.Precision = 6;
options.Stages = 6;
Set variables type option (boolean):
options.Types = 1;
Optimize problem:
[Objectives, UB_Init_Capital, Points, GraphHandle2]=riskconstrparam ([],'linear', [], [], [], [], ... 0.0000001, matrix_costs, [], [], matrix_NPV, UB_Init_Capital(1), [], [], [], [], point_lowerbounds, point_upperbounds, 'r', [],[],[],... [], [], UB_Init_Capital, [], options); |
Describe output arguments of PSG subroutine riskconstrparam:
Output argument |
Meaning |
Objectives |
row vector of the optimal values of the objective found by optimizing the problem for each parameter value; |
UB_Init_Capital |
row vector of values for right-hand side of constraint on available capital (CS.2); |
Points |
matrix of optimal points found by optimizing the problem for each parameter; |
GraphHandle2 |
handle of the graphical object (if option.PlotGraph = ‘On’, otherwise GraphHandle = [] ). |
Solution of optimization problem is in Table 1 and on Figure 1.
Load data from mat file:
load('CS_Project_Selection_FXCHG_riskconstrprog_data.mat');
Specifies a set of values of parameter (upper bound on init capital) for which runs should be conducted:
UB_Init_Capital = [300 350 400 500 600 650];
Set solver options:
options.Linearization = 'On';
options.Solver = 'CAR';
options.Precision = 6;
options.Stages = 6;
Optimize problem:
[Objectives, UB_Init_Capital, Points, GraphHandle]=riskconstrparam ([],'fxchg_pos', [], [], [], [], ... 0.0000001, matrix_costs, [], [], matrix_NPV, UB_Init_Capital(1), [], [], [], [], point_lowerbounds, point_upperbounds, 'r', [],[],[],... [], [], UB_Init_Capital, [], options); |
Describe output arguments of PSG subroutine riskconstrparam:
Output argument |
Meaning |
Objectives |
row vector of the optimal values of the objective found by optimizing the problem for each parameter value; |
UB_Init_Capital |
row vector of values for right-hand side of constraint on available capital (CS.5); |
Points |
matrix of optimal points found by optimizing the problem for each parameter; |
GraphHandle |
handle of the graphical object (if option.PlotGraph = ‘On’, otherwise GraphHandle = [] ). |
Solution of optimization problem is in Table 2 and on Figure 1.
Table 1. Solution of Problem 1
UB_Init_Capital 300 350 400 500 600 650
Objective 460.0000 510.0000 540.0000 610.0000 640.0000 660.0000
Optimal points
Project
Project1 1.000000 1.000000 1.000000 1.000000 1.000000 1.000000
Project2 0.000000 0.000000 1.000000 0.000000 1.000000 0.000000
Project3 1.000000 1.000000 1.000000 1.000000 1.000000 1.000000
Project4 1.000000 1.000000 1.000000 1.000000 1.000000 1.000000
Project5 0.000000 1.000000 1.000000 1.000000 1.000000 1.000000
Project6 0.000000 0.000000 0.000000 1.000000 1.000000 1.000000
Project7 0.000000 0.000000 0.000000 0.000000 0.000000 1.000000
Table 2. Solution of Problem 2
B_Init_Capital 300 350 400 500 600 650
Objective 430.0000 510.0000 540.0000 610.0000 640.0000 660.0000
Optimal points
Project
Project1 1.000000 1.000000 1.000000 1.000000 1.000000 1.000000
Project2 1.000000 0.000000 1.000000 0.000000 1.000000 0.000000
Project3 1.000000 1.000000 1.000000 1.000000 1.000000 1.000000
Project4 0.000000 1.000000 1.000000 1.000000 1.000000 1.000000
Project5 0.000000 1.000000 1.000000 1.000000 1.000000 1.000000
Project6 0.000000 0.000000 0.000000 1.000000 1.000000 1.000000
Project7 0.000000 0.000000 0.000000 0.000000 0.000000 1.000000
Figure 1. Objective vs Parameter for Problem 1 and Problem 2