Description

MATLAB code

Problem 1

Problem 2

Results

Table 1. Solution of Problem 1

Table 2. Solution of Problem 2

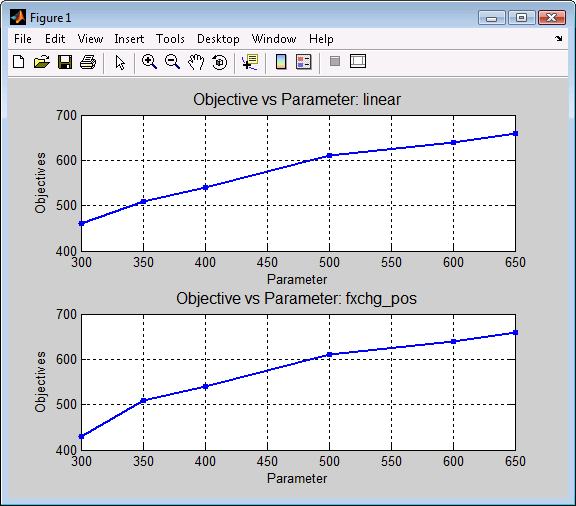
Figure 1. Objective vs Parameter for Problem 1 and Problem 2

 

Description

Problem of optimization setup for a project selection problem in MATLAB Environment.  Two optimization problems (see Formal Problem Statement) Problem 1 (CS.1) - (CS.3) and Problem 2 (CS.4) - (CS.6) are solved in General text format by tbpsg_run.

Main MATLAB code is in file CS_Project_Selection_FXCHG_tbpsg_run.m.

Data are saved in file CS_Project_Selection_FXCHG_tbpsg_run_data.mat.

 

MATLAB code

Let us describe the main operations. To run case study you need to do the following main steps:

 

In file CS_Project_Selection_FXCHG_tbpsg_run.m.

 

Problem 1

 

Load data from mat file:

 

load(CS_Project_Selection_FXCHG_tbpsg_run_data.mat');

tbpsg_export_to_workspace(toolboxstruc_arr);

 

Specify the set of values of upper bound on available initial capital:

 

UB_Init_Capital = [300 350 400 500 600 650];

Objectives(6) =0;

 

Begin loop for Optimization Problem 1 over parameter values:

 

for i=1:1:length(UB_Init_Capital)

 

Generate problem statement:

 

   clear problem_statement;

   problem_statement = sprintf('%s\n',...

  'maximize',...

  '  linear(matrix_CS_Project_Selection_npv)',...

   ['Constraint: constraint_budget_linear, <=  ',num2str(UB_Init_Capital(i)),', linearize = 1'],...

  '  linear(matrix_CS_Project_Selection_costs)',...

  'Box: >= point_lowerbounds, <= point_upperbounds , types = 1',...

  '');

 

% Uncomment the following line to open the problem in Toolbox Window:

% tbpsg_toolbox(problem_statement,toolboxstruc_arr);

 

Optimize problem:

 [solution_str, outargstruc_arr] = tbpsg_run(problem_statement, toolboxstruc_arr);

 

Extract optimal solution:

 

   point_variables = tbpsg_optimal_point_vars(solution_str, outargstruc_arr);

   Points_Problem_1(:,i) = tbpsg_optimal_point_data(solution_str, outargstruc_arr)';

   Objectives(i) = tbpsg_objective(solution_str, outargstruc_arr);

   constr_function_value = tbpsg_constraints_data(solution_str, outargstruc_arr);  

 

end

 

Solution of optimization problem is in Table 1 and on Figure 1.

 

Problem 2

 

Load data from mat file:

 

load(CS_Project_Selection_FXCHG_tbpsg_run_data.mat');

tbpsg_export_to_workspace(toolboxstruc_arr);

 

Specify the set of values of upper bound on available initial capital:

 

UB_Init_Capital = [300 350 400 500 600 650];

Objectives(6) =0;

 

Begin loop for Optimization Problem 2 over parameter values:

 

for i=1:length(UB_Init_Capital)

 

Generate problem statement:

 

   clear problem_statement;

   problem_statement = sprintf('%s\n',...

  'maximize',...

  '  linear(matrix_cs_project_selection_npv)',...

   ['Constraint: constraint_budget, <=  ',num2str(UB_Init_Capital(i)),', linearize = 1'],...

  '  fxchg_pos(0.0000001, matrix_cs_project_selection_costs)',...

  'Box: >= point_lowerbounds, <= point_upperbounds',...  

  '');

 

% Uncomment the following line to open the problem in Toolbox Window:

% tbpsg_toolbox(problem_statement,toolboxstruc_arr);

 

Optimize problem:

 [solution_str, outargstruc_arr] = tbpsg_run(problem_statement, toolboxstruc_arr);

 

Extract optimal solution:

   point_variables = tbpsg_optimal_point_vars(solution_str, outargstruc_arr);

   Points_Problem_2(:,i) = tbpsg_optimal_point_data(solution_str, outargstruc_arr)';

   Objectives(i) = tbpsg_objective(solution_str, outargstruc_arr);

   constr_function_value = tbpsg_constraints_data(solution_str, outargstruc_arr);  

 

end

 

Solution of optimization problem is in Table 2 and on Figure 1.

 

 

Results

Table 1. Solution of Problem 1

 

UB_Init_Capital         300         350         400         500         600         650

Objective            460.0000    510.0000    540.0000    610.0000    640.0000    660.0000

Optimal points

Project

Project1            1.000000    1.000000    1.000000    1.000000    1.000000    1.000000

Project2            0.000000    0.000000    1.000000    0.000000    1.000000    0.000000

Project3            1.000000    1.000000    1.000000    1.000000    1.000000    1.000000

Project4            1.000000    1.000000    1.000000    1.000000    1.000000    1.000000

Project5            0.000000    1.000000    1.000000    1.000000    1.000000    1.000000

Project6            0.000000    0.000000    0.000000    1.000000    1.000000    1.000000

Project7            0.000000    0.000000    0.000000    0.000000    0.000000    1.000000

 

Table 2. Solution of Problem 2

 

B_Init_Capital         300         350         400         500         600         650

Objective            430.0000    510.0000    540.0000    610.0000    640.0000    660.0000

Optimal points

Project

Project1            1.000000    1.000000    1.000000    1.000000    1.000000    1.000000

Project2            1.000000    0.000000    1.000000    0.000000    1.000000    0.000000

Project3            1.000000    1.000000    1.000000    1.000000    1.000000    1.000000

Project4            0.000000    1.000000    1.000000    1.000000    1.000000    1.000000

Project5            0.000000    1.000000    1.000000    1.000000    1.000000    1.000000

Project6            0.000000    0.000000    0.000000    1.000000    1.000000    1.000000

Project7            0.000000    0.000000    0.000000    0.000000    0.000000    1.000000

 

Figure 1. Objective vs Parameter for Problem 1 and Problem 2