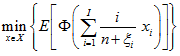Background

Problem. Stochastic Utility (or Expected Utility) Problem which is approximated by sampling stochastic parameters of this problem

Simplified Problem Statement

Mathematical Problem Statement

Problem dimension and solving time

Solution in Run-File Environment

Solution in MATLAB Environment

References

 

Background

 

This case study solves Stochastic Utility (or Expected Utility) Problem which is approximated by sampling stochastic parameters of this problem (Sampling Average Approximation approach). The problem formulation and data are based on dataset which is considered in Nemirovski et al. (2009). The dataset was provided for testing purposes by Prof. George Lan. The problem formulation, as presented in Nemirovski et al. (2009), is as follows

 

 

An equivalent formulation to (CS.0) in terms of PSG functions is presented in approximation format with scenarios in (CS.1-CS.3) (see Formal Problem Statement).

 

The Case Study presents solved problem instance with 500 variables and 4000 scenarios with sampled random coefficients, .

 

Problem

 

Simplified Problem Statement

 

Minimize Avg_max_risk (minimizing average of maximum of random linear functions)

 subject to

linear ≤ 1 (budget constraint on sum of variables)

Box constraints (variables are not negative)

 

where

 

Avg_max_risk = Average Max Risk for Loss

Box constraints = constraints on individual decision variables

 

Mathematical Problem Statement

 

 

Problem dimension and solving time

 

 

Solution in Run-File Environment

 

 

Input Files to run CS:

 

Output Files:

 

Solution in MATLAB Environment

 

Solved with PSG MATLAB function tbpsg_run (General (Text) Format of PSG in MATLAB):

 

 

Input Files to run CS:

 

References

 

[1] Nemirovski A., Juditsky A., Lan G. and A. Shapiro (2009): Robust stochastic approximation approach to Stochastic programming, SIAM J. Optim., Vol. 19, No. 4, 1574-1609.