Syntax

Logistic function applied to a Linear function:

 

 

Logistic function applied to Sum of Splines Operator:

 

 

Parameters

matrix        is a Matrix of Scenarios:

       

 

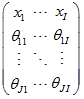
Note. The scenario_probability, and scenario_benchmark columns may be included in matrix but are not used in calcuations.

 

matrix_param, matrix_data, and matrix_knots are parameters of Sum of Splines Operator.

 

Mathematical Definition

1. Logistic function applied to a Linear function is a vector function with components:

, ,

where , .

Remarks

In order to include the intercept in the polynomial , one should assign .  In this case, the matrix of scenarios should be set as follows:

  .

 

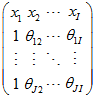2. Logistic function applied to Sum of Splines Operator is a vector function with components:

, ,

where , described in Sum of Splines Operator. One Independent Factor.

 

Example

 

See also

Loss, Gain, Sum of Splines Operator, Logarithms Exponents Sum