Quick Start with PSG MATLAB
Initiation steps:
1. Verify that MATLAB version is 7.2 or higher.
2. Install Portfolio Safeguard (PSG).
3. Verify paths in MATLAB to the folder containing PSG libraries '...\Aorda\PSG\MATLAB' and '...\Aorda\PSG\MATLAB\Tools'.
As example, we consider Conditional Value-at-Risk minimization, and show main steps in PSG MATLAB environment:
Conditional Value-at-Risk minimization. Mathematical formulation
This example demonstrates CVaR (see PSG Function cvar_risk) minimization with average (expected) return (see PSG Function avg_g) and budget constraints.
General mathematical formulation of the minimization problem:
![]()
subject to
portfolio return constraint:
![]()
budget constraint:
![]()
bounds on decision variables:
![]()
where
![]() = vector of decision variables;
= vector of decision variables;
![]() = portfolio return of instruments;
= portfolio return of instruments;
![]() = Conditional Value-at-Risk for return;
= Conditional Value-at-Risk for return;
![]() = average return.
= average return.
PSG functions in CVaR minimization problem:
1. Conditional Value-at-Risk in PSG is named "CVaR Risk for Loss" (see cvar_risk). Function call :
cvar_risk(α, matrix)
where
![]() = confidence level,
= confidence level,
matrix = matrix of scenarios (see Matrix of Scenarios) with rows containing returns of instruments, benchmarks and probabilities.
Inputs for cvar_risk:
| • | Confidence level: |
![]() ;
;
| • | Matrix: |
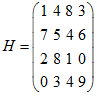
| • | Benchmark vector: |
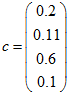
| • | Probabilities vector: |
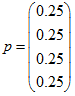
2. Average ( Expected value) of random linear gains in PSG is called Average Gain (see avg_g). Function call:
avg_g(matrix)
where
matrix = matrix of scenarios (see Matrix of Scenarios) with rows containing returns of instruments, benchmarks and probabilities.
Inputs for avg_g:
H, c, p are the same as in cvar_risk function.
There are three possibilities for optimizing this problem in PSG MATLAB environment: PSG Toolbox GUI, Special PSG MATLAB Subroutines and Programmatical PSG.
Example 1. Conditional Value-at-Risk Minimization. Toolbox
See also:
Example 2. Conditional Value-at-Risk Minimization. Special Subroutines
Firstly, CVaR is minimized with PSG Subroutine riskconstrprog (see riskconstrprog).
Remarks
| • | PSG Subroutine Riskconstrprog solves risk minimization problems with constraint on risk function and linear constraints. If the constraint on risk function is absent, use PSG Subroutine Riskprog (see riskprog); |
| • | risk constraint for Riskconstrprog should be upper bounded. So, inequality |
Define input data in MATLAB:
H = [1,4,8,3; 7,5,4,6; 2,8,1,0; 0,3,4,9];
c = [0.2; 0.11; 0.6; 0.1];
p=[0.25,0.25,0.25,0.25]; %Can be set p=[], because probabilities are equal.
Aeq = [1, 1, 1, 1];
beq = 1;
r = -4.5;
lb = [0; 0; 0; 0];
Run subroutine (see riskconstrprog function):
[xout, fval, status, output] = riskconstrprog('cvar_risk', 'avg', 0.95, H, c, p, [], H, c, p, [], r, [], [], Aeq, beq, lb);
Output:
Optimal point:
xout =
0
0.6000
0.1900
0.2100
Objective value on the optimal point:
fval =
-4.3500
Status of the solved optimization problem:
status =
optimal
Full report for solution of the optimization problem:
output =
xout: [4x1 double]
fval: -4.3500
frval1: -4.3500
fdval: []
frval2: -4.5000
fAval: []
rAval: []
fAeqval: 1.0000
rAeqval: 4.4409e-016
data_loading_time: 0.0100
preprocessing_time: 0
solving_time: 0
MATLAB code for CVaR minimization using riskconstrprog is in: ./Aorda/PSG/MATLAB/Examples/Problems/Example_CVaR_riskconstrprog.m.
Example 3. Conditional Value-at-Risk Minimization. Programmatical PSG
Define input data in MATLAB:
H=[1,4,8,3; 7,5,4,6; 2,8,1,0; 0,3,4,9];
c=[0.2; 0.11; 0.6; 0.1];
p=[];
Aeq=[1, 1, 1, 1];
lb=[0; 0; 0; 0];
vars={'x1', 'x2', 'x3', 'x4'};
Pack data to PSG Data Objects and save them to array of structures toolboxstruc_arr:
Pack input data to PSG structure containing matrix headers and data (see PSG Data Objects in MATLAB).
Pack matrices to the elements of the array "toolboxstruc_arr" (see function tbpsg_matrix_pack):
toolboxstruc_arr(1) = tbpsg_matrix_pack('matrix_scenarios',H,vars,c,p);
toolboxstruc_arr(2) = tbpsg_matrix_pack('matrix_budget',Aeq,vars);
Pack point to the elements of the array "toolboxstruc_arr" (see function tbpsg_point_pack):
toolboxstruc_arr(3) = point_pack('point_lowerbounds',lb,vars);
Create string with Problem Statement (see Problem Statement in MATLAB):
problem_statement = sprintf('%s\n',...
'minimize',...
'cvar_risk(0.95, matrix_scenarios)',...
'Constraint: >= 4.5',...
'avg_g(matrix_scenarios)',...
'Constraint: == 1',...
'linear(matrix_budget)',...
'Box: >= point_lowerbounds');
Solve problem with tbpsg_run:
[solution_str, outargstruc_arr] = mpsg_solver(problem_statement,toolboxstruc_arr)
You will get the following output (see PSG Solution in MATLAB):
Full report for the solution of the optimization problem: (Full report with the optimization problem solution)
solution_str =
Problem: solution_status = optimal
Timing: Data_loading_time = 0.18, Preprocessing_time = 0.00, Solving_time = 0.00
Variables: optimal_point = point_problem_1
Objective: = -4.350000000000
Constraint: constraint_1 = 4.500000000000e+000, [0.000000000000e+000]
Constraint: constraint_2 = 1.000000000000e+000, [-4.440892098501e-016]
Function: avg_g(matrix_scenarios) = 4.500000000000e+000
Function: cvar_risk(0.95,matrix_scenarios) = -4.350000000000e+000
Function: linear(matrix_budget) = 1.000000000000e+000
Optimal point in PSG point format (see PSG Point in MATLAB):
outargstruc_arr =
object_name: 'point_problem'
variables: 'x1 x2 x3 x4'
type: 'point'
values: [0 0.6000 0.1900 0.2100]
Convert PSG solution to structure (see tbpsg_solution_struct):
>> output_structure = tbpsg_solution_struct(solution_str, outargstruc_arr)
output_structure =
status: {'optimal'}
time: [0.2200 0 0]
objective: -4.3500
function_name: {3x1 cell}
function_value: [3x1 double]
vector_function_name: {}
vector_function_value: {}
optimal_point_data: [0 0.6000 0.1900 0.2100]
optimal_point_vars: {'x1' 'x2' 'x3' 'x4'}
point_constraint_data: [4.5000 1.0000]
point_constraint_vars: {'constraint_1' 'constraint_2'}
point_slack_data: [0 -4.4409e-016]
point_dual_data: [3.7037 -22.1111]
vector_constraints_data: {}
vector_slack_data: {}
vector_dual_data: {}
matrix_data: {}
matrix_vars: {}
vector_data: {}
MATLAB code for CVaR minimization is in: ./Aorda/PSG/MATLAB/Examples/Problems/Example_CVaR_General.m.
