Sum of Splines in Calculation
Contents
Spline_Sum Operator is a scenario function with vector output (see Extended Mathematical Definition).
calculate
point: point_spline
spline_sum(matrix_param, matrix_data, matrix_knots) |
short call; |
spline_sum_name(matrix_param, matrix_data, matrix_knots) |
call with optional name. |
point_spline point with two columns defining spline coefficients:
where
first row is predefined (see PSG Point);
= names of variables defining splines coefficients, 
= spline number, 
= piece number, 
= number of coefficient in polynomial.
matrix_param is a PSG matrix with spline parameters:
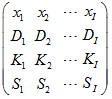
where
header row contains names of factors 
. Other rows contain numerical data:
= degrees of polynomial function for each factor.
= numbers of pieces for each factor.
= smoothing degree for each factor.
matrix_data is a Matrix of Scenarios with observations of dependent (scenario_benchmark) and independent variables:
where
header row contains names of variables (except scenario_probability, and scenario_benchmark). Other rows contain numerical data. The scenario_probability column is optional.
Spline_Sum is calculated at every observation of dependent variable 
.
matrix_knots is a PSG matrix with predefined knots of splines:
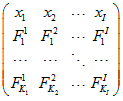
where
header row contains names of factors. Other rows contain numerical data (knots values).
Remarks
| • | matrix_knots contain (user specified) values of knots and this matrix is required (not optional); |
| • | number of knot values in one column of matrix_knots may differ from the number of knot values in another column ( ). In this case shorter columns must be supplemented with zeros. |
solution_status calulated = spline are set correctly, infeasible = splines inputs are not consistent.
vector_spline_sum vector of residuals (difference of observed and predicted spline values):
where
first row is predefined (see PSG Vector);
(see Extended Mathematical Definition) .
point_problem_calculate initials values of coefficients of spline (coincides with input point point_spline).
constraint_for_smoothing_spline maximum modulus value of the constraints and it's maximal deviation from zero (in square brackets) (see Additional constraints in Optimization problem).
Examples of Calculating Spline Sum
Consider problem of spline_sum calculation on matrix matrix_data. Coefficients of splines (point_spline) obtained by maximization of PSG function Logarithms Exponents Sum (see Examples of Optimization Problem).
Problem Statement:
calculate
point: point_problem_logexp_of_spline
spline_sum(matrix_vars_f1, matrix_data_f1, matrix_data_f1_knots)
Output in Run-File environment:
File "solution_problem_calculate.txt":
Problem: solution_status = calculated
Timing: Data_loading_time = 0.03, Preprocessing_time = 0.00, Solving_time = 0.00
Variables: optimal_point = point_problem_calculate
Objective: = 0.000000000000
Constraint: constraint_for_smoothing_spline = -9.228173780684e-013 [9.228173780684e-013]
Function: spline_sum(matrix_vars_f1, matrix_data_f1, matrix_data_f1_knots) = vector_spline_sum
Note
| • | solution_status = calculated if input spline coefficients satisfies Additional constraints in Optimization problem, otherwise solution_status = infeasible |
| • | Objective equals 0 if input spline coefficients satisfies Additional constraints in Optimization problem. |
File "point_problem_calculate.txt":
Component_name Value
f1_1_0 5.115949156682e-001
f1_1_1 1.363516222718e+000
f1_1_2 8.496803299671e-001
f1_1_3 1.593553645899e-001
f1_2_0 -1.796809664083e-001
f1_2_1 -2.682444790951e-001
f1_2_2 -4.342465155557e-001
f1_2_3 -1.773909370834e-001
f1_3_0 -1.774649056175e-001
f1_3_1 -2.220196383596e-001
f1_3_2 -1.128449983675e-001
f1_3_3 5.675111084198e-001
f1_4_0 -7.238952502380e-002
f1_4_1 -9.180786847385e-001
f1_4_2 1.424141094563e+000
f1_4_3 -5.637752204972e-001
f1_5_0 -3.762511948285e+000
f1_5_1 7.294872709909e+000
f1_5_2 -4.668933233238e+000
f1_5_3 9.430137919686e-001
Note. This point coincides with input point point_problem_logexp_of_spline.
File "vector_spline_sum.txt":
Value
1.141854524163e+000
2.797490076146e-001
1.133451735849e+000
1.372389025502e-001
1.149555961273e+000
1.644250986223e-001
2.484441485041e-001
...